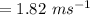Question

A student m1 = 71 kg runs towards his skateboard, which has a mass m2 = 2.8 kg and is d = 2.75 m ahead of him. He begins at rest and accelerates at a constant rate of a = 0.65 m/s2. When he reaches the skateboard he jumps on it. What is the velocity of the student and skateboard in meters per second?

Answer 1

The velocity of the student and skateboard together
`=1.82\ ms^(-1)`

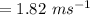
Step-by-step explanation:

Given:

Mass of student
`m_1=71\ kg`

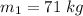
Mass of skateboard
`m_2=2.8\ kg`

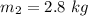
Distance between student and skateboard
`d=2.75\ m`

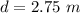
Acceleration of student
`a=0.65\ ms^(-2)`

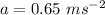
Finding velocity
`v_1` of the student before jumping on skateboard

Using equation of motion

`v_1^2=v_0^2+2ad`

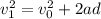
here
`v_0` represents the initial velocity of the student which is
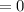`=0` as he starts from rest.

So,

`v_1^2=0^2+2(0.65)(2.75)`

`v_1^2=3.575`

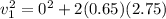
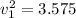
Taking square root both sides:

`√(v_1^2)=\sqrt[1.7875}`

∴
`v_1=1.89`

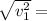
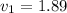
Finding velocity
`v` of student and skateboard.

Using law of conservation of momentum.

`m_1v_1+m_2v_2=(m_1+m_2)v`

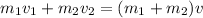
Where
`v_2` is initial velocity of skateboard which is
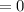`=0` as it is at rest.

Plugging in values.

`71(1.89)+(2.8)(0)=(71+2.8)\ v`

`134.19=73.8\ v`

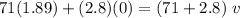
Dividing both sides by
`73.8`

`(134.19)/(73.8)=(73.8\ v)/(73.8)`

∴
`v=1.82`

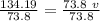
The velocity of the student and skateboard together
`=1.82\ ms^(-1)`