Answer:
0.024 m = 24.07 mm
Step-by-step explanation:
1) Notation
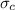 = tensile stress = 200 Mpa
= tensile stress = 200 Mpa
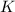 = plane strain fracture toughness= 55 Mpa
= plane strain fracture toughness= 55 Mpa
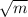
 = length of a surface crack (Variable of interest)
= length of a surface crack (Variable of interest)
2) Definition and Formulas
The Tensile strength is the ability of a material to withstand a pulling force. It is customarily measured in units (F/A), like the pressure. Is an important concept in engineering, especially in the fields of materials and structural engineering.
By definition we have the following formula for the tensile stress:
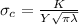 (1)
(1)
We are interested on the minimum length of a surface that will lead to a fracture, so we need to solve for

Multiplying both sides of equation (1) by
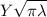
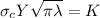 (2)
(2)
Sequaring both sides of equation (2):
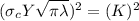
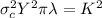 (3)
(3)
Dividing both sides by
 we got:
we got:
![\lambda=(1)/(\pi)[(K)/(Y\sigma_c)]^2](https://img.qammunity.org/2020/formulas/engineering/college/sa3uqssulzh23re1ojqhgliozd4zppzr0t.png) (4)
(4)
Replacing the values into equation (4) we got:
![\lambda=(1)/(\pi)[(55 Mpa√(m))/(1.0(200Mpa))]^2 =0.02407m](https://img.qammunity.org/2020/formulas/engineering/college/89d5g5ehqunf029bwhok9oyk9lggvc3ig6.png)
3) Final solution
So the minimum length of a surface crack that will lead to fracture, would be 24.07 mm or more.