Answer:
"To the nearest year, it would be about 9 years"
Explanation:
11c)
This is compound growth problem. It goes by the formula:

Where
F is the future amount
P is the present (initial) amount
r is the rate of growth, in decimal
t is the time in years
Given,
P = 20,000
r = 8% = 8/100 = 0.08
F = double of initial amount = 2 * 20,000 = 40,000
We need to find t:

To solve exponentials, we can take Natural Log (Ln) of both sides:
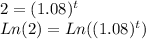
Using the rule shown below we can simplify and solve:
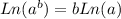
We can write:
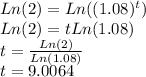
To the nearest year, that would be about 9 years