Answer:
a) mean= 158.4 , standard deviation = 3.394
b) Best option : B. Yes, since the original population is normal, the sampling distribution of the sum will also be approximately normal.
c) P(X>160) = P(Z>0.471) = 1-P(Z<0.471) = 0.3188
Explanation:
1) Notation
n = sample size = 8
 = population mean = 19.8
= population mean = 19.8
 = population standard deviation = 1.2
= population standard deviation = 1.2
2) Definition of the variable of interest
Part a
The variable that we are interested is
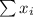 and the mean and the deviation for this variable are given by :
and the mean and the deviation for this variable are given by :
E(
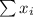 ) =
) =
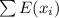 = n
= n
 = 8x19.8 = 158.4
= 8x19.8 = 158.4
Var(
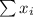 ) =
) =
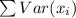 = n
= n

Sd(
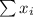 ) =
) =
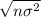 =
=
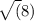 x 1.2 = 3.394
x 1.2 = 3.394
Part b
For this case the populations are normal, then the distribution for the sample (
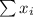 ) is normal too.
) is normal too.
Based on this the distribution for the variable X would be normal, so the best option should be:
B. Yes, since the original population is normal, the sampling distribution of the sum will also be approximately normal.
Part c
From part a we know that the mean = 158.4 and the deviation = 3.394
The z score is defined as
Z = (X -mean)/ deviation = (160-158.4)/ 3.394 = 0.471
Then we can find the probability P(X>160) = P(Z>0.471) = 1-P(Z<0.471) = 0.3188