Answer:
Angular displacement of the wheel,
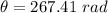
Step-by-step explanation:
It is given that,
Angular acceleration of the wheel,

Final speed of the wheel,
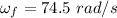
Time taken, t = 4.5 s
Initially, it is required to find the initial angular velocity of the wheel. Using the first equation of rotational kinematics as :
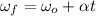
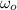 is the initial speed of the wheel
is the initial speed of the wheel
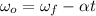


Let
 is the angular displacement of each wheel during this time. Using the second equation of motion as :
is the angular displacement of each wheel during this time. Using the second equation of motion as :
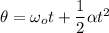

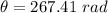
So, the angular displacement of each wheel during this time is 267 radian.