Question

A production process fills containers by weight. Weights of containers are approximately normally distributed. Historically, the standard deviation of weights is 5.5 ounces. (This standard deviation is therefore known.) A quality control expert selects n containers at random. How large a sample would be required in order for the 99% confidence interval for to have a length of 2 ounces?

a. n  15
b. n  16
c. n  201
d. n  226

Answer 1

option (c) n = 201

Explanation:

Data provided in the question:

Standard deviation, s = 5.5 ounce

Confidence level = 99%

Length of confidence interval = 2 ounces

Therefore,

margin of error, E = (Length of confidence interval ) ÷ 2

= 2 ÷ 2

= 1 ounce

Now,

E =
`(zs)/(\sqrt n)`

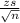
here,

z = 2.58 for 99% confidence interval

n = sample size

thus,

1 =
`(2.58*5.5)/(\sqrt n)`

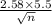
or

n = (2.58 × 5.5)²

or

n = 201.3561 ≈ 201

Hence,

option (c) n = 201