Answer:
The numerical value of the trigonometric function is 30 °
Explanation:
Given trigonometric function as :
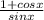 +
+
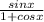 = 4
= 4
or, Taking LCM we get
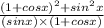 = 4
= 4
Or, ( 1 + cos x )² + sin² x = 4 × ( sin x ) × ( 1 + cos x )
1 + cos² x + 2 cox + sin² x = 4 sin x + 4 sin x × cos x
or, ( cos² x + sin² x ) + ( 1 + 2 cos x ) = 4 sin x ( 1 + cos x )
∵ cos² x + sin² x = 1
or, 1 + 1 + 2 cos x = 4 sin x ( 1 + cos x )
or, 2 + 2 cos x = 4 sin x ( 1 + cos x )
or, 2 ( 1 + cos x ) = 4 sin x ( 1 + cos x )
Or,
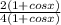 = sin x
= sin x
Or, sin x =
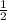
∴ x =
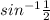
∵ sin 30 ° =
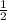
I.e x = 30 °
Hence The numerical value of the trigonometric function is 30 ° answer