Answer:
The speed v of the particle at t=5.00 seconds = 43 m/s
Step-by-step explanation:
Given :
mass m = 5.00 kg
force f(t) = 6.00t2−4.00t+3.00 N
time t between t=0.00 seconds and t=5.00 seconds
From mathematical expression of Newton's second law;
Force = mass (m) x acceleration (a)
F = ma
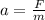 ...... (1)
...... (1)
acceleration (a)
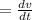 ......(2)
......(2)
substituting (2) into (1)
Hence, F
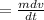
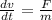
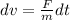
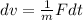
Integrating both sides
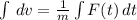
The force is acting on the particle between t=0.00 seconds and t=5.00 seconds;
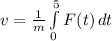 ......(3)
......(3)
Substituting the mass (m) =5.00 kg of the particle, equation of the varying force f(t)=6.00t2−4.00t+3.00 and calculating speed at t = 5.00seconds into (3):
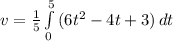
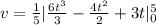
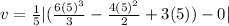
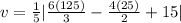
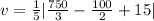
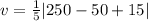
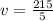
v = 43 meters per second
The speed v of the particle at t=5.00 seconds = 43 m/s