Question

A solid circular plate has a mass of 0.25 kg and a radius of 0.30 m. It starts rolling from rest at the top of a hill 10 m long and inclined at 30o to the horizontal. What will the speed of the plate be at the bottom of the hill if it rolls without slipping? Think of the plate as a short solid cylinder.

A. 2.7 m/s
B. 6.9 m/s
C. 8.1 m/s
D. 3.3 m/s
E. 10.4 m/s

Answer 1

To solve the problem it is necessary to apply the equations related to the conservation of both kinetic of rolling objects and potential energy and the moment of inertia.

The net height from the point where it begins to roll with an inclination of 30 degrees would be

`h=Lsin30`

`h=10sin30`

`h=5m`

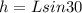
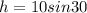
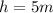
In the case of Inertia would be given by

`I = (mR^2)/(2)`

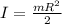
In general, given an object of mass m, an effective radius k can be defined for an axis through its center of mass, with such a value that its moment of inertia is

`I = mk^2`

`(mR^2)/(2)= mk^2`

`(k^2)/(R^2)=(1)/(2)`

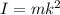
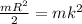
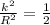
Replacing in Energy conservation Equation we have that

Potential Energy = Kinetic Energy of Rolling Object

`mgh = (1)/(2)mv^2(1+(k^2)/(r^2))`

`9.8*5=(1)/(2)v^2(1+(1)/(2))`

`v^2 (1.5) = 98`

`v=8.0829m/s`

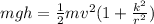
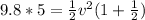
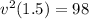
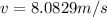
Therefore the correct answer is C.