Question

A research firm conducted a survey to determine the mean amount Americans spend on coffee during a week. They found the distribution of weekly spending followed the normal distribution with a population standard deviation of $5. A sample of 64 Americans revealed that X¯¯¯=$20 . What is the 95% confidence interval estimate of μ?

Answer 1

The confidence interval is between 18.775 and 21.225.

Explanation:

Answer 2

95% confidence Interval would be between $18.775 and $20.225.

Explanation:

Confidence Interval can be calculated using M±ME where

• M is the sample mean Americans spend on coffee during week. ($20)

• ME is the margin of error from the mean

And margin of error (ME) around the mean calculated as

ME=
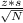`(z*s)/(√(N) )` where

• z is the corresponding statistic in 95% confidence level (1.96)

• s is the population standard deviation ($5)

• N is the sample size (64)

Using the numbers, we get:

ME=
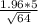`(1.96*5)/(√(64) )` =1.225

Then 95% confidence Interval would be 20±1.225 or between $18.775 and $20.225