Question

A ladder 10 ft long leans against a vertical wall. If the bottom of the ladder slides away from the base of the wall at a speed of 2 ft/s, how fast is the angle between the ladder and the wall changing when the bottom of the ladder is 6 ft from the base of the wall?

Answer 1

`(dx)/(dt)=(-8)/(3)(ft)/(s)`

Explanation:

Be
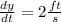`(dy)/(dt)=2(ft)/(s)` to find
`(dx)/(dt)=?, x=6ft`

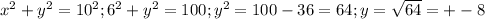`x^(2) +y^(2)=10^(2);6^(2)+y^(2)=100;y^(2)=100-36=64;y=√(64)=+-8`→ y=8 for being the positive distance, deriving from t,
`x^(2) +y^(2)=100`→
`2x(dx)/(dt)+2y(dy)/(dt)=0`→
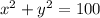`2x(dx)/(dt)=-2y(dy)/(dt);(dx)/(dt)=-(2y)/(2x)(dy)/(dt); (dx)/(dt)=-(y)/(x)(dy)/(dt)`, if x=6 and y=8

`(dx)/(dt)=(-8)/(6)2`→
`(dx)/(dt)=(-8)/(3)(ft)/(s)`

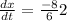we must find the rate of change in radians over seconds, being the speed 8/3 ft / s = 2.66 ft / s the variation in degrees is determined when traveling 6 ft