Answer:
a)
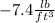
b)
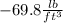
c)

Step-by-step explanation:
1) Notation
 represent the shear stress defined as "the external force acting on an object or surface parallel to the slope or plane in which it lies"
represent the shear stress defined as "the external force acting on an object or surface parallel to the slope or plane in which it lies"
R represent the radial distance
L the longitude
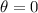 since at the begin we have a horizontal pipe, but for parts b and c the angle would change.
since at the begin we have a horizontal pipe, but for parts b and c the angle would change.
D represent the diameter for the pipe
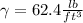 is the specific weight for the water
is the specific weight for the water
2) Part a
For this case we can use the shear stress and the radial distance to find the pressure difference per unit of lenght, with the following formula
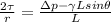
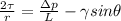
If we convert the difference's into differentials we have this:
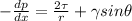
We can replace
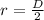 and we have this:
and we have this:
![(dp)/(dx)=-[(4\tau)/(D)+\gamma sin\theta]](https://img.qammunity.org/2020/formulas/engineering/college/qkthbr46rhh4pcfcppdf0zd4846yi19bwn.png)
Replacing the values given we have:
![(dp)/(dx)=-[(4x1.85(lb)/(ft^2))/(1ft)+62.4(lb)/(ft^3) sin0]=-7.4(lb)/(ft^3)](https://img.qammunity.org/2020/formulas/engineering/college/hay58uoa9cqc5ske4ibxelgrfxxkchs9in.png)
3) Part b
When the pipe is on vertical upward position the new angle would be
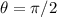 , and replacing into the formula we got this:
, and replacing into the formula we got this:
![(dp)/(dx)=-[(4x1.85(lb)/(ft^2))/(1ft)+62.4(lb)/(ft^3) sin90]=-69.8(lb)/(ft^3)](https://img.qammunity.org/2020/formulas/engineering/college/ygnri11v97jlho58dk6lzbt391msn30gdp.png)
4) Part c
When the pipe is on vertical downward position the new angle would be
 , and replacing into the formula we got this:
, and replacing into the formula we got this:
![(dp)/(dx)=-[(4x1.85(lb)/(ft^2))/(1ft)+62.4(lb)/(ft^3) sin(-90)]=55 (lb)/(ft^3)](https://img.qammunity.org/2020/formulas/engineering/college/wax4joee5dtnwuuxb2pjn26jsi9gfe2c6k.png)