Step-by-step explanation:
Relation between entropy change and specific heat is as follows.

The given data is as follows.
mass = 500 g,
 = 24.4 J/mol K
= 24.4 J/mol K
 = 500 K,
= 500 K,
 = 250 K
= 250 K
Mass number of copper = 63.54 g /mol
Number of moles =
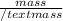
=

= 7.86 moles
Now, equating the entropy change for both the substances as follows.
![7.86 * 24.4 * [T_(f) - 250]](https://img.qammunity.org/2020/formulas/chemistry/high-school/bo8nr5be0migeakhapar12n5wjyfjco465.png) =
=
![7.86 * 24.4 * [500 -T_(f)]](https://img.qammunity.org/2020/formulas/chemistry/high-school/3pfrrwhajw5qo6he5rh66lldyyjho71396.png)

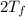 = 750
= 750
So,
 =
=

- For the metal block A, change in entropy is as follows.

=
![24.4 log [(375)/(500)]](https://img.qammunity.org/2020/formulas/chemistry/high-school/mpoqbn586fjs824ka2j9d3jtbovlw45ac7.png)
= -3.04 J/ K mol
- For the block B, change in entropy is as follows.

=
![24.4 log [(375)/(250)]](https://img.qammunity.org/2020/formulas/chemistry/high-school/3roxlc1q1xls67y2cgwr6v376qvjy6s10z.png)
= 4.296 J/Kmol
And, total entropy change will be as follows.
= 4.296 + (-3.04)
= 1.256 J/Kmol
Thus, we can conclude that change in entropy of block A is -3.04 J/ K mol and change in entropy of block B is 4.296 J/Kmol.