Question

In a rural area, only about 30% of the wells that are drilled find adequate water at a depth of 100 feet or less. A local man claims to be able to find water by "dowsing"—using a forked stick to indicate where the well should be drilled. You check with 80 of his customers and find that 27 have wells less than 100 feet deep. What do you conclude about his claim?

a) Write appropriate hypotheses.
b) Check the necessary assumptions.
c) Perform the mechanics of the test. What is the P-value?
d) Explain carefully what the P-value means in context. e) What’s your conclusion?

Answer 1

Explanation:

Given that in a rural area, only about 30% of the wells that are drilled find adequate water at a depth of 100 feet or less.

The sample size n = 80

no of wells less than 100 feet deep=27

Sample proportion =
`(27)/(80) =0.3375`

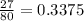
a) Create hypotheses as

`H_0: p = 0.30\\H_a: p >0.30\\`

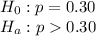
(Right tailed test)

p difference
`= 0.3375-0.30 = 0.0375`

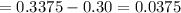
Std error of p =
`\sqrt{(0.3(0.7))/(80) } =0.0512`

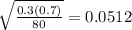
b) Assumptions: Each trial is independent and np and nq >5

c) Z test can be used.

Z= p diff/std error =
`(0.0375)/(0.0512) =0.73`

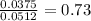
p value = 0.233

d) p value is the probability for which null hypothesis is false.

e) Conclusion: Since p >0.05 we accept null hypothesis

there is no statistical evidence which support the claim that more than 30% are drilled.