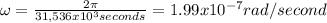Question

Calculate the angular velocity of the earth in its orbit around the sun.

Answer 1

`0.0172rad/day=1.99x10^(-7)rad/second`

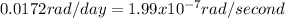
Step-by-step explanation:

The definition of angular velocity is as follows:

`\omega=2\pi f`

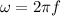
where
`\omega` is the angular velocity, and
`f` is the frequency.

Frequency can also be represented as:

`f=(1)/(T)`

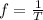
where
`T` is the period, (the time it takes to conclude a cycle)

with this, the angular velocity is:

`\omega=(2\pi)/(T)`

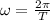
The period T of rotation around the sun 365 days, thus, the angular velocity:

`\omega=(2\pi)/(365days)=0.0172rad/day`

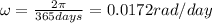
if we want the angular velocity in rad/second, we need to convert the 365 days to seconds:

Firt conveting to hous

`365days((24hours)/(1day) )=8760hours`

then to minutes

`8760hours((60minutes)/(1hour) )=525,600minutes`

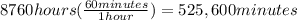
and finally to seconds

`525,600minutes((60seconds)/(1minute))=31,536x10^3seconds`

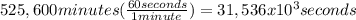
thus, angular velocity in rad/second is:

`\omega=(2\pi)/(31,536x10^3seconds)=1.99x10^(-7)rad/second`