Question

A North-South road meets an East-West road at an intersection. At a certain moment, a car on the North-South road is 4 miles north of the intersection and is traveling north at 55 miles per hour. At the same moment, a truck on the East-West road is 3 miles east of the intersection and is traveling east at 45 miles per hour. How fast is the distance between the car and the truck increasing at that moment?

Answer 1

The distance 5 miles North-East of the intersection between the car and the truck increasing at 71.06 miles per hour at that moment.

Explanation:

Looking at the attached figures, Fig 1 shows the diagram of the car and the truck.

Using Pythagoras theorem on Fig 1a,

`l^(2) = \sqrt{3^(2) + 4^(2) }`

`l = √(9 +16) \\\\l= √(25) \\\\l = 5 miles`

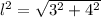
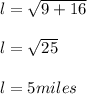
The resultant displacement between the car and the truck at that same moment is 5 miles.

From the velocity vector diagram on Fig 2,

The resultant velocity R is given as

`R = \sqrt{45^(2) + 55^(2) }\\\\R = √(2025 + 3025 )\\\\R = √(5050 )\\\\R = 71.06mph`

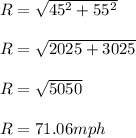
Therefore, the distance 5 miles North-East of the intersection between the car and the truck increasing at 71.06 miles per hour at that moment.