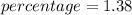Answer:
Part a)

Part B)
percentage increase is
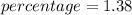 %
%
Step-by-step explanation:
Part a)
As we know that the beat frequency is
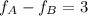
after increasing the tension the beat frequency is decreased and hence the tension in string B will increase
So we have
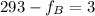

Part B)
percentage increase in the tension of the string will be given as
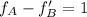
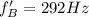
now we have
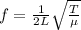
so we have
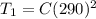
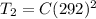
so we have
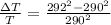
percentage increase is