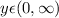Question

Simplify the function f(x) = 1/3 (81) 3x/4 Then determine the key aspects of the function.

Answer 1

Answer: 1/3 27 all real numbers y>0

Explanation:

Answer 2

`f(x)=3^(3x-1)`.

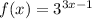The domain of the function is the set of all real number and the range is
`(0,\infty)`

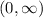
Explanation:

Given:

The function is given as:

`f(x)=(1)/(3)(81)^{(3x)/(4)}`

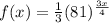
Using the rule of the exponents,
`a^(mn)=(a^m)^n`,

`f(x)=(1)/(3)((81)^{(1)/(4)})^((3x))\\f(x)=(1)/(3)(\sqrt[4]{81} )^(3x)\\f(x)=(1)/(3)(3)^(3x)\\f(x)=(3^(3x))/(3^1)`

Using the rule of the exponents,
`(a^m)/(a^n)=a^(m-n)`,

`f(x)=3^(3x-1)`

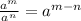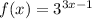
Therefore, the simplified form of the given function is:

`f(x)=3^(3x-1)`

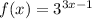
Key aspects:

The given function is an exponential function with a constant base 3.

Domain is the set of all possible values of
`x` for which the function is defined.

The domain of an exponential function is a set of all real values.

The range of an exponential function is always greater than zero.

Therefore, the domain of this function is also all real values and the range is from 0 to infinity.

Domain:
`x \epsilon (-\infty,\infty)`

Range:
`y\epsilon (0,\infty)`