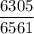Answer: a)
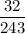 b)
b)
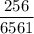 c)
c)
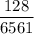 d)
d)
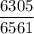
Explanation:
Since we have given that
Probability that each person agrees independently to be interviewed =

(a) 5 names?
If it has 5 names, then the probability would be

(b) What if it has 8 names?
If it has 8 names, then the probability would be
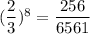
(c) If the list has 8 names what is the probability that the reviewer will contact exactly 7 people in completing her assignment?

(d) With 8 names, what is the probability that she will complete the assignment without contacting every name on the list?
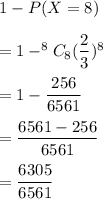
Hence, a)
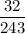 b)
b)
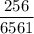 c)
c)
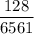 d)
d)