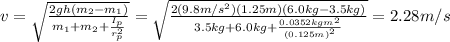Answer:
Step-by-step explanation:
For the first mass we have
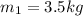 , and for the second
, and for the second
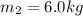 . The pulley has a moment of intertia
. The pulley has a moment of intertia
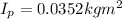 and a radius
and a radius
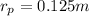 .
.
We solve this with conservation of energy. The initial and final states in this case, where no mechanical energy is lost, must comply that:
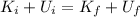
Where K is the kinetic energy and U the gravitational potential energy.
We can write this as:
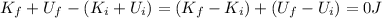
Initially we depart from rest so
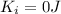 , while in the final state we will have both masses moving at velocity v and the tangential velocity of the pully will be also v since it's all connected by the string, so we have:
, while in the final state we will have both masses moving at velocity v and the tangential velocity of the pully will be also v since it's all connected by the string, so we have:
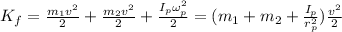
where we have used the rotational kinetic energy formula and that
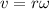
For the gravitational potential energy part we will have:
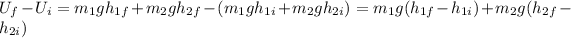
We don't know the final and initial heights of the masses, but since the heavier,
 , will go down and the lighter,
, will go down and the lighter,
 , up, both by the same magnitude h=1.25m (since they are connected) we know that
, up, both by the same magnitude h=1.25m (since they are connected) we know that
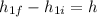 and
and
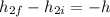 , so we can write:
, so we can write:
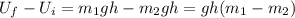
Putting all together we have:
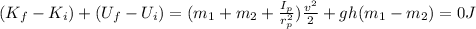
Which means: