Answer:
(0.4062, 0.5098)
Explanation:
In a sample with a number n of people surveyed with a probability of a success of
 , and a confidence interval
, and a confidence interval
 , we have the following confidence interval of proportions.
, we have the following confidence interval of proportions.
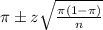
In which
Z is the zscore that has a pvalue of

For this problem, we have that:
356 dies were examined by an inspection probe and 163 of these passed the probe. This means that
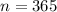 and
and

Assuming a stable process, calculate a 95% (two-sided) confidence interval for the proportion of all dies that pass the probe.
So
 = 0.05, z is the value of Z that has a pvalue of
= 0.05, z is the value of Z that has a pvalue of
![1 - (0.05)/(2) = 0.975[tex], so [tex]z = 1.96](https://img.qammunity.org/2020/formulas/mathematics/college/va5srpiemdrsx997nsq89s2purivhsfold.png) .
.
The lower limit of this interval is:
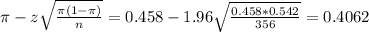
The upper limit of this interval is:

The correct answer is
(0.4062, 0.5098)