Answer:
a)
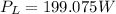
b)
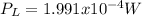
Step-by-step explanation:
1) Notation
Power on the refrigerator:

Voltage
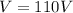
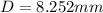 , so then the radius would be
, so then the radius would be
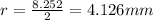
 , representing the length of the two wires.
, representing the length of the two wires.
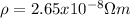 , that represent the resistivity for the aluminum founded on a book
, that represent the resistivity for the aluminum founded on a book
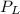 power lost in the transmission.
power lost in the transmission.
2) Part a
We can find the total power adding all the individual values for power:
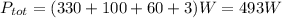
From the formula of electric power:
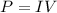
We can solve for the current like this:
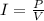
Since we know
 and the voltage 110 V, we have:
and the voltage 110 V, we have:
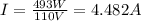
The next step would be find the cross sectional are for the aluminum cables with the following formula:
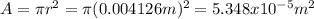
Then with this area we can find the resistance for the material given by:

With this resistance then we can find the power dissipated with the following formula:
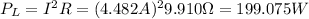
And if we want to find the percentage of power loss we can use this formula
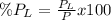
3) Part b
Similar to part a we just need to change the value for V on this case to 110KV.
We can solve for the current like this:
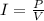
Since we know
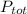 and the voltage 110 KV=110000V, we have:
and the voltage 110 KV=110000V, we have:
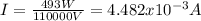
The cross sectional area is the same
The resistance for the material not changes.
With this resistance then we can find the power dissipated with the following formula:
