Question

A system has three macrostates. Macrostates 1 and 3 are least likely and have one basic state each. Macrostate 2 is the equilibrium state and is four times more likely to occur than either of the other two macrostates.

Part A
What is the probability that the equilibrium state 2 occurs?
Express your answer using three significant digits.
p2=
Part B
What is the probability that macrostate 1 occurs?
Express your answer using three significant digits.
p1=
Part C
What is the probability that macrostate 3 occurs?
Express your answer using three significant digits.
p3=
Part D
What is the sum of the probabilities for all macrostates?
Express your answer using three significant digits.
p=

Answer 1

`p2=0.667\\p1=0.167\\p3=0.167\\p=1`

Step-by-step explanation:

Let's start writing the sample space for this exercise :

Let be ''M'' an abbreviation for Macrostate

Ω = { M1 , M2 , M3 }

Let be P(M1) the probability of Macrostate 1.

Reading the exercise, we know that ⇒

`P(M1)=P(M3)`

Let's note this probability as ''p''.

`P(M1)=P(M3)=p`

Macrostate 2 is four times more likely to occur than either of the other two macrostates ⇒

`P(M2)=4p`

The sum of all probabilities must be equal to 1 for this sample space.Therefore,

`p+p+4p=1`

`6p=1`

`p=(1)/(6)`

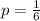
Finally :

`P(M1)=(1)/(6)`

`P(M2)=(4)/(6)`

`P(M3)=(1)/(6)`

For Part A :

`p2=(4)/(6)=0.667`

For Part B and C :

`p1=p3=0.167`

For Part D :

The sum of the probabilities for all macrostates is equal to 1 :

`p=p1+p2+p3=(1)/(6)+(4)/(6)+(1)/(6)=(6)/(6)=1`