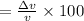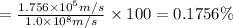Question

An atom of silver has a radius of and the average orbital speed of the electrons in it is about . Calculate the least possible uncertainty in a measurement of the speed of an electron in an atom of silver. Write your answer as a percentage of the average speed, and round it to significant digits.

Answer 1

Percentage of uncertainty in average speed of an electron is 0.1756%.

Step-by-step explanation:

Using Heisenberg uncertainty principle:

`\Deltax* \Delta p\geq (h)/(4\pi )`

`\Delta p=m* \Delta v`

`\Deltax* m* \Delta v\geq (h)/(4\pi )`

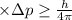
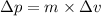
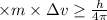
Δx = Uncertainty in position

Δp = Uncertainty in momentum

Δv = Uncertainty in average speed

h = Planck's constant =
`6.626* 10^(-34) kg m^2/s`

m = mass of electron =
`9.1* 10^(-31) kg`

We have

Δx = 2 × 165 pm = 330 pm =
`3.3* 10^(-10) m`

`1 pm = 10^(-12) m`

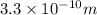
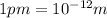
Average orbital speed of electron = v =
`=1.0* 10^8 m/s`

`3.3* 10^(-10) 9.1* 10^(-31) kg * \Delta v\geq (6.626* 10^(-34) kg m^2/s)/(4\pi )`

`\Delta v\geq (6.626* 10^(-34) kg m^2/s)/(4\pi * 3.3* 10^(-10)* 9.1* 10^(-31) kg)`

`\Delta v\geq 1.756* 10^5 m/s`

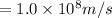
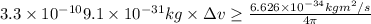
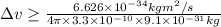
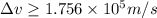
Percentage of uncertainty in average speed:

`=(\Delta v)/(v)* 100`

`=(1.756* 10^5 m/s)/(1.0* 10^8 m/s)* 100=0.1756\%`