Answer:
A.

Explanation:
Given:
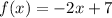
The function
 is shifted 6 units below which forms the function
is shifted 6 units below which forms the function

To find the function
 , we apply the following translation rules:
, we apply the following translation rules:
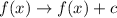
If
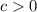 the function
the function
 shifts
shifts
 units up.
units up.
If
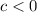 the function
the function
 shifts
shifts
 units down.
units down.
Since the function
 is shifting 6 units below, thus value of
is shifting 6 units below, thus value of
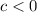 which is taken as -6.
which is taken as -6.
The translation occurring here is given by:
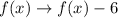
Thus,
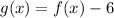
Substituting
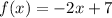
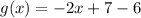
∴
