Answer:
a) I = 13.77 A
b) 0 ° or to the East
Step-by-step explanation:
Part a
The magnetic field by properties would be 0 at the radius on this case r =8.1 cm.Analyzing the situation the wirde would produce a magnetic field equals in magnitude to the magnetic field on Earth by with the inverse direction.
The formula for the magnetic field due to a wire with current is:
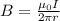
In order to have a value of 0 for the magnetic field at the radius then we need to have this balance
B (r=8.1) = B (Earth)
Replacing:
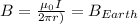
Solving from I, from the last equation we got:
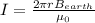
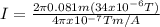 = 13.77 A
= 13.77 A
Part b
We can use the right hand rule for this case.
The magnetic field of the wire would point to the South, because the magnetic field of the earth given points to the North. Based on this the current need's to flow from West to East in order to create a magnetic field pointing to the south, because the current would be perpendicular to the magnetic field created.