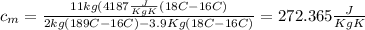Answer:
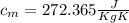
Step-by-step explanation:
1) Notation and data given
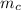 = mass of the container = 3.9 kg
= mass of the container = 3.9 kg
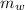 = mass of the water inside of the container= 11 kg
= mass of the water inside of the container= 11 kg
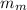 =mass of the metal= 2 kg
=mass of the metal= 2 kg
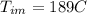 initital temperature of the metal
initital temperature of the metal
 initital temperature of the water
initital temperature of the water
 initital temperature of the container
initital temperature of the container
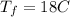 final equilibrium temperature
final equilibrium temperature
2) Concepts and formulas
Since the inital temperature for the pice of metal is higher than the temperature for the container and the water inside, the piece of metal will transfer heat, and this transferred heat is the same amount absorbed by the container and the water reaching the equilibrium. So then we have this formula:
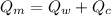
We don't have any change of phase so then we just have the presence of sensible heat, and using this we got that:
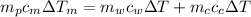
On this case the container is made by the same metal so then
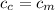
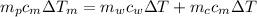
And solving for
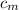 from the last expression we got:
from the last expression we got:
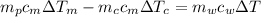
![c_m [m_p \Delta T_m -m_c \Delta T_c] =m_w c_w \Delta T](https://img.qammunity.org/2020/formulas/physics/high-school/4xfw4ppo6g6o9gatoz3hd0g8zos5hsmv8t.png)

Replacing the values we have: