Question

Water flows in a constant diameter pipe with the following conditions measured:

At section (a) pa = 31.1 psi and za = 56.7 ft; at section (b) pb = 27.3 psi and zb = 68.8 ft.
(a) Determine the head loss from section (a) to section (b).
(b) Is the flow from (a) to (b) or from (b) to (a)?

Answer 1

a)
`h_L=-3.331ft`

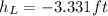
b) The flow would be going from section (b) to section (a)

Step-by-step explanation:

1) Notation

`p_a =31.1psi=4478.4(lb)/(ft^2)`

`p_b =27.3psi=3931.2(lb)/(ft^2)`

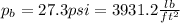
For above conversions we use the conversion factor
`1psi=144(lb)/(ft^2)`

`z_a =56.7ft`

`z_a =68.8ft`

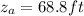
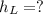`h_L =?` head loss from section

2) Formulas and definitions

For this case we can apply the Bernoulli equation between the sections given (a) and (b). Is important to remember that this equation allows en energy balance since represent the sum of all the energies in a fluid, and this sum need to be constant at any point selected.

The formula is given by:

`(p_a)/(\gamma)+(V_a^2)/(2g)+z_a =(p_b)/(\gamma)+(V_b^2)/(2g)+z_b +h_L`

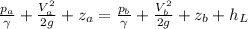
Since we have a constant section on the piple we have the same area and flow, then the velocities at point (a) and (b) would be the same, and we have just this expression:

`(p_a)/(\gamma)+z_a =(p_b)/(\gamma)+z_b +h_L`

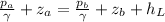
3)Part a

And on this case we have all the values in order to replace and solve for
`h_L`

`(4478.4(lb)/(ft^2))/(62.4(lb)/(ft^3))+56.7ft=(3931.2(lb)/(ft^2))/(62.4(lb)/(ft^3))+68.8ft +h_L`

`h_L=(71.769+56.7-63-68.8)ft=-3.331ft`

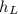
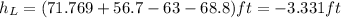
4)Part b

Analyzing the value obtained for
`\h_L` is a negative value, so on this case this means that the flow would be going from section (b) to section (a).