Question

Before hanging new William Morris wallpaper in her bedroom, Brenda sanded the walls lightly to smooth out some irregularities on the surface. The sanding block weighs 2.30 N and Brenda pushes on it with a force of 3.00 N at an angle of 30.0° with respect to the vertical, and angled toward the wall. What is the coefficient of kinetic friction between the wall and the block?

Answer 1

To solve the exercise it is necessary to apply the equations necessary to apply Newton's second law and the concept related to frictional force.

An angle of 30 degrees is formed on the vertical at an applied force of 2.3N

In this way the frictional force, opposite to the movement will be given by

`f_k = \mu_k N`

where,

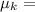`\mu_k =` Kinetic friction constant

N = Normal Force (Mass*gravity)

The friction force is completely vertical and opposes the rising force of 2.3 N. The Normal force acts perpendicular to the surface (vertical) therefore corresponds to the horizontal component of the applied force.

The ascending force would be given by

`F_v = 2.3N*Cos30 = 1.99N`

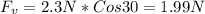
As the block is moving upward, the friction force acts downward, also its weight acts downward. We can have

`2.3N+f_k = 1.99N`

`f_k = 0.31N`

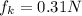
Considering the horizontal force the normal force on the block must be balanced by the horizontal component of pishing foce

`N = 2.3sin30`

`N = 1.15N`

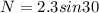
Then the frictional force

`f_k = \mu_k N`

`0.31N = \mu_k 1.15`

`\mu_k = (0.31)/(1.15)`

`\mu_k =0.26`

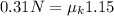
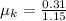
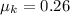
Therefore the coefficient of kinetic friction is 0.26