Question

On the basis of data collected during an experiment, a biologist found that the growth of a fruit fly population (Drosophila) with a limited food supply could be approximated by

N(t) = 600/1+39e^-0.16t
(a) What was the initial fruit fly population in the experiment? where t denotes the number of days since the beginning of the experiment.
(b) What was the population of the fruit fly colony on the t = 11 day? (Round your answer to the nearest integer.)

Answer 1

(a). 15

(b). 78

Explanation:

Growth of the population of a fruit fly is modeled by

N(t) =
`(600)/(1+39e^(-0.16t) )`

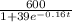
where t = number of days from the beginning of the experiment.

(a). For t = 0 [Initial population]

N(0) =
`(600)/(1+39e^(-0.16* 0) )`

=
`(600)/(1+39)`

=
`(600)/(40)`

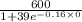
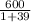
= 15

Initial population of the fruit flies were 15.

(b).Population of the fruit fly colony on 11th day.

N(11) =
`(600)/(1+39e^(-0.16* 11) )`

=
`(600)/(1+39e^(-1.76) )`

=
`(600)/(1+39* 0.172 )`

=
`(600)/(1+6.71)`

=
`(600)/(7.71)`

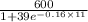
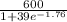
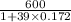
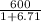
= 77.82

≈ 78

On 11th day number of fruit flies colony were 78.