Answer:
a)
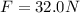
b)
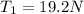
c)
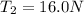
d)
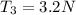
Step-by-step explanation:
Let's do the free body diagram per each body. In this particular case the rope has a mass so we have:
First block
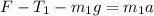 (1)
(1)
Frist rope
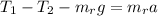 (2)
(2)
Second block
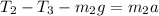 (3)
(3)
Second rope
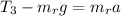 (4)
(4)
When,
T
₁ is the tension at the top of the rope 1
T
₂ is the tension at the bottom of the rope 1
T
₃ is the tension at the top of the rope 2
Now, if we add all equations from (1) to (4), we will get the value of F,

a) Solving this equation for F:
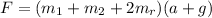
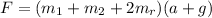
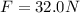
b) Using the equation (1), we can find T₁
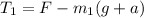
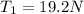
c) Let's use the equation (2) to find T₂
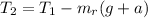
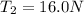
d) Using the equation (4) we can find T₃:
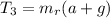
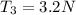
Have a nice day!