Answer:
The expression simplifies to
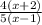 .
.
Explanation:
The expression
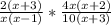
can be rearranged and written as
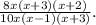
In this form the
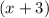 terms in the numerator and in the denominator cancel to give
terms in the numerator and in the denominator cancel to give
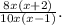
The
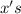 are present both in the numerator and in the denominator, so they also cancel, and the fraction
are present both in the numerator and in the denominator, so they also cancel, and the fraction
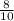 simplifies to
simplifies to
 , so finally our expression becomes:
, so finally our expression becomes:
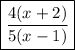
Which is our answer:)