Question

A bowl in the shape of a hemispere is filled with water to a depth h=3 inches. The radius of the bowl is R inches. Express the radius of the bowl R as a function of the angle theta.

Answer 1

The radius of the bowl R as a function of the angle theta is
`\mathrm{R}=(3)/(1-\sin \theta)`

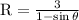
Solution:

The figure is attached below

If we consider the centre of hemisphere be A

The radius be AC and AD

According to question,

A bowl in the shape of a hemispere is filled with water to a depth h=3 inches .i.e. BC = h = 3 inches

And radius of the bowl is R inches .i.e. R = AD =AC

Now , using trigonometric identities in triangle ABD we get

`\sin \theta=\frac{\text { Perpendicular }}{\text { Hypotenuse }}=(A B)/(A D)`

`\begin{array}{l}{\sin \theta=(A B)/(R)} \\\\ {A B=R \sin \theta}\end{array}`

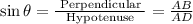
Since , AC = AB + BC

R = R Sinθ + 3

R - R Sinθ = 3

R (1 – Sinθ ) = 3

`\mathrm{R}=(3)/(1-\sin \theta)`

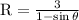
Which is the required expression for the radius of the bowl R as a function of the angle theta