For this case we must find the solution of the following system of inequalities:
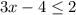 or
or
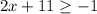
Inequality 1:
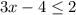
We add 4 to both sides of the inequality:
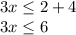
We divide between 3 on both sides of the inequality:
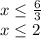
Thus, the solution is given by all values of x less than or equal to 2.
Inequality 2:
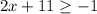
We subtract 11 from both sides of the inequality:

We divide between 2 on both sides of the inequality:

Thus, the solution is given by all values of x greater than or equal to -6.
Thus, the solution set is given by:
(-∞, - 2] U [-6,∞)
That is, the solution set is given by all real numbers.
Answer:
All real numbers