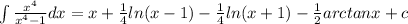Answer:
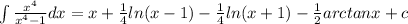
Explanation:
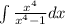
Adding and Subtracting 1 to the Numerator
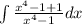
Dividing Numerator seperately by
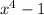
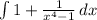
Here integral of 1 is x +c1 (where c1 is constant of integration
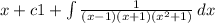 ----------------------------------(1)
----------------------------------(1)
We apply method of partial fractions to perform the integral
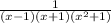 =
=
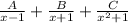 ------------------------------------------(2)
------------------------------------------(2)
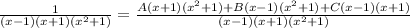
1 =
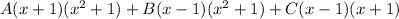 -------------------------(3)
-------------------------(3)
Substitute x= 1 , -1 , i in equation (3)
1 = A(1+1)(1+1)
A =
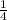
1 = B(-1-1)(1+1)
B =
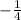
1 = C(i-1)(i+1)
C =
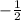
Substituting A, B, C in equation (2)
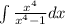 =
=
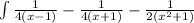
On integration
Here
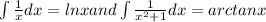
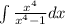 =
=
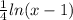 -
-
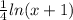 -
-
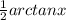 + c2---------------------------------------(4)
+ c2---------------------------------------(4)
Substitute equation (4) back in equation (1) we get
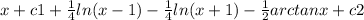
Here c1 + c2 can be added to another and written as c
Therefore,