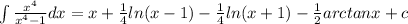Question

Please, I need help in this ??

Answer 1

`\int(x^(4))/(x^(4) -1)dx = x + (1)/(4) ln(x-1) - (1)/(4) ln(x+1)-(1)/(2) arctanx + c`

Explanation:

`\int(x^(4))/(x^(4) -1)dx`

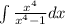
Adding and Subtracting 1 to the Numerator

`\int(x^(4) - 1 + 1)/(x^(4) -1)dx`

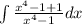
Dividing Numerator seperately by
`x^(4) - 1`

`\int 1 + (1)/(x^(4)-1 )\, dx`

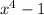
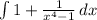
Here integral of 1 is x +c1 (where c1 is constant of integration

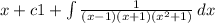`x + c1 + \int(1)/((x-1)(x+1)(x^(2)+1))\, dx`----------------------------------(1)

We apply method of partial fractions to perform the integral

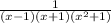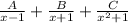`(1)/((x-1)(x+1)(x^(2)+1))` =
`(A)/(x-1) + (B)/(x+1) + (C)/(x^(2) + 1)`------------------------------------------(2)

`(1)/((x-1)(x+1)(x^(2)+1)) = (A(x+1)(x^(2) +1) + B(x-1)(x^(2) +1) + C(x-1)(x+1))/((x-1)(x+1)(x^(2) +1))`

1 =
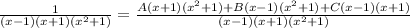
`A(x+1)(x^(2) +1) + B(x-1)(x^(2) +1) + C(x-1)(x+1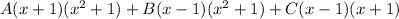)`-------------------------(3)

Substitute x= 1 , -1 , i in equation (3)

1 = A(1+1)(1+1)

A =
`(1)/(4)`

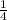
1 = B(-1-1)(1+1)

B =
`-(1)/(4)`

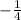
1 = C(i-1)(i+1)

C =
`-(1)/(2)`

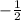
Substituting A, B, C in equation (2)

`\int(x^(4))/(x^(4) -1)dx` =
`\int(1)/(4(x-1)) - (1)/(4(x+1)) -(1)/(2(x^(2)+1) )`

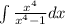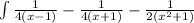
On integration

Here
`\int (1)/(x)dx = lnx and \int(1)/(x^(2)+1 ) dx = arctanx`

`\int(x^(4))/(x^(4) -1)dx` =
`(1)/(4) ln(x-1)` -
`(1)/(4) ln(x+1)` -
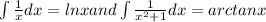
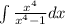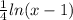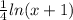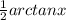`(1)/(2) arctanx` + c2---------------------------------------(4)

Substitute equation (4) back in equation (1) we get

`x + c1 + (1)/(4) ln(x-1) - (1)/(4) ln(x+1) - (1)/(2) arctanx + c2`

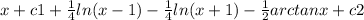
Here c1 + c2 can be added to another and written as c

Therefore,

`\int(x^(4))/(x^(4) -1)dx = x + (1)/(4) ln(x-1) - (1)/(4) ln(x+1)-(1)/(2) arctanx + c`