Answer:
Yes, those are the first triangular numbers.
There is a relation between the number and its position but isn't direct.
Explanation:
The triangular numbers can be represented by equilateral triangles, but also can be represented by:
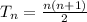
where:
n, represents the position
T represent the triangular number.
As you may see, the equation of triangular numbers is not a straight line. It is a parable. For that reason there isn't a direct variation.