Answer: 98% confidence interval is (0.06,0.11).
Explanation:
Since we have given that
Number of men = 550
Number of women = 2400
Number of men have color blindness = 48
Number of women have color blindness = 5
So,

So, at 98% confidence interval, z = 2.326
so, interval would be
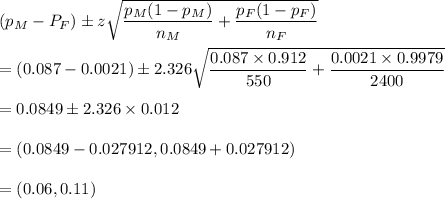
Hence, 98% confidence interval is (0.06,0.11).
No, there does not appears to be a significant difference.