Question

Find the common ratio and the three terms in the sequence after the last one given. -4, 16, -64, 256, …

Answer 1

The ratio of all the adjacent terms is the same and equal to

`r=-4`

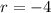
The next three terms after the last one will be:

• 
  `a_5=-1024`

• 
  `a_6=4096`

• 
  `a_7=-16384`

Explanation:

Given the sequence

-4, 16, -64, 256, …

Finding the common ratio

An arithmetic sequence has a constant ratio 'r' and is defined by

`a_n=a_1\cdot r^(n-1)`

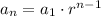
computing the ratios of all the adjacent terms

`(16)/(-4)=-4,\:\quad (-64)/(16)=-4,\:\quad (256)/(-64)=-4`

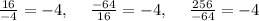
The ratio of all the adjacent terms is the same and equal to

`r=-4`

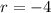
Finding the next three terms

Given the sequence

-4, 16, -64, 256, …

here

`a_1=-4`

`r=-4`

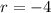
substituting
`a_1=-4` and
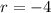`r=-4` in the nth term

`a_n=a_1\cdot r^(n-1)`

`a_n=-4\left(-4\right)^(n-1)`

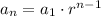
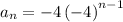
substituting n = 5 to determine the 5th term

`a_5=-4\left(-4\right)^(5-1)`

`a_5=-4^4\cdot \:4`

`\mathrm{Apply\:exponent\:rule}:\quad \:a^b\cdot \:a^c=a^(b+c)`

`a_5=-4^(1+4)`

`a_5=-4^5`

`a_5=-1024`

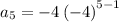
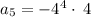
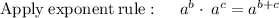
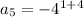
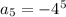
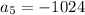
substituting n = 6 to determine the 6th term

`a_6=-4\left(-4\right)^(6-1)`

`a_6=-4\left(-4^5\right)`

`\mathrm{Apply\:rule}\:-\left(-a\right)=a`

`a_6=4\cdot \:4^5`

`\mathrm{Apply\:exponent\:rule}:\quad \:a^b\cdot \:a^c=a^(b+c)`

`a_6=4^(1+5)`

`a_6=4^6`

`a_6=4096`

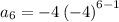
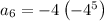
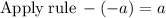
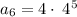
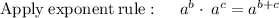
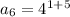
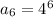
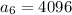
substituting n = 7 to determine the 6th term

`a_7=-4\left(-4\right)^(7-1)`

`a_7=-4^6\cdot \:4`

`\mathrm{Apply\:exponent\:rule}:\quad \:a^b\cdot \:a^c=a^(b+c)`

`a_7=-4^(1+6)`

`a_7=-4^7`

`a_7=-16384`

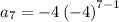
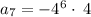
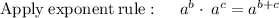
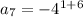
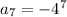
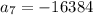
Therefore, the next three terms after the last one will be:

• 
  `a_5=-1024`

• 
  `a_6=4096`

• 
  `a_7=-16384`