Question

In professional basketball games during 2009-2010, when Kobe Bryant of the Los Angeles Lakers shot a pair of free throws, 8 times he missed both, 152 times he made both, 33 times he only made the first, and 37 times he made the second. Is it plausible that the successive free throws are independent?

Answer 1

Is plausible that the successive throws are independent

Explanation:

1) Table with info given

The observed values are given by the following table

__________________________________________________

First shot Made Second shot missed Total

__________________________________________________

Made 152 33 185

Missed 37 8 45

__________________________________________________

Total 189 41 230

2) Calculations and test

We are interested on check independence and for this we need to conduct a chi square test, the next step would be find the expected value:

Null hypothesis: Independence between two successive free throws

Alternative hypothesis: No Independence between two successive free throws

_____________________________________________________

First shot Made Second shot missed

_____________________________________________________

Made 189(185)/230=152.0217 41(185)/230=32.9783

Missed 189(45)/230=36.9783 41(45)/230=8.0217

_____________________________________________________

On this case all the expected values are higher than 5 and the sample size 230 is enough to apply the chi squared test.

3) Calculate the chi square statistic

The statistic for this case is given by:

`\chi_(cal)^2 =\sum ((O_i -E_i))/(E_i)`

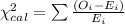
Where O represent the observed values and E the expected values. Replacing the values that we got we have this

`\chi_(cal)^2 =((152-152.0217)^2)/(152.0217)+((33-32.9783)^2)/(32.9783)+((37-36.9783)^2)/(36.9783)+((8-8.0217)^2)/(8.0217)=0.000003098+0.00001428+0.00001273+0.0.00005870=0.00008881`

Now with the calculated value we can find the degrees of freedom

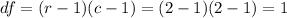`df=(r-1)(c-1)=(2-1)(2-1)=1` on this case r means the number of rows and c the number of columns.

Now we can calculate the p value

`p_v =P(\chi^2 >0.00008881)=0.9925`

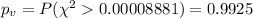
On this case the pvalue is a very large value and that indicates that we can fail to reject the null hypothesis of independence. So is plausible that the successive throws are independent.