Question

Please answer! I crossed out the ones you don’t have to complete.

Answer 1

1. Rewriting the expression 5.a.b.b.5.c.a.b.5.b using exponents we get:
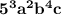
`\mathbf{5^3a^2b^4c}`

5.
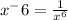
`x^-6 = (1)/(x^6)`

6.
`5^(-3).3^(-1)=(1)/(5^3.3^1)`

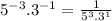
7.
`a^(-3)b^0c^4=(c^4)/(a^3)`

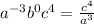
Explanation:

Question 1:

We need to rewrite the expression using exponents

5.a.b.b.5.c.a.b.5.b

We will first combine the like terms

5.5.5.a.a.b.b.b.b.c

Now, if we have 5.5.5 we can write it in exponent as:
`=5^(1+1+1)=5^3`

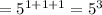
a.a as
`a^(1+1)=a^2`

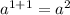
b.b.b.b as:
`b^(1+1+1+1)=b^4`

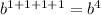
So, our result will be:

`5^3a^2b^4c`

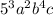
Rewriting the expression 5.a.b.b.5.c.a.b.5.b using exponents we get:
`\mathbf{5^3a^2b^4c}`

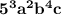
Question:

Rewrite using positive exponent:

The rule used here will be:
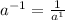`a^(-1)=(1)/(a^1)` which states that if we need to make exponent positive, we will take it to the denominator.

Applying thee above rule for getting the answers:

5)
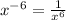
`x^(-6) = (1)/(x^6)`

6)
`5^(-3).3^(-1)=(1)/(5^3.3^1)`

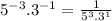
7)
`a^(-3)b^0c^4=(b^0c^4)/(a^3)`

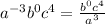
We know that
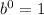`b^0=1` so, we get

`a^(-3)b^0c^4=(b^0c^4)/(a^3)=(c^4)/(a^3)`