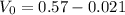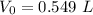Answer:
1)
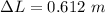
2) a.

b.

c.
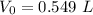
Step-by-step explanation:
1)
- given initial length,
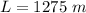
- initial temperature,
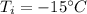
- final temperature,
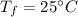
- coefficient of linear expansion,
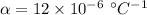
∴Change in temperature:


We have the equation for change in length as:
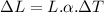
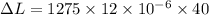
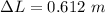
2)
Given relation:
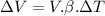
where:
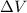 = change in volume
= change in volume
V= initial volume
 =change in temperature
=change in temperature
- initial volume of tank,
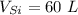
- initial volume of gasoline,

- initial temperature of steel tank,
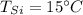
- initial temperature of gasoline,
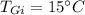
- coefficients of volumetric expansion for gasoline,
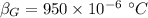
- coefficients of volumetric expansion for gasoline,

a)
final temperature of gasoline,
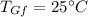
∴Change in temperature of gasoline,
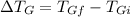
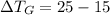
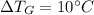
Now,

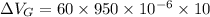

b)
final temperature of tank,

∴Change in temperature of tank,
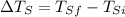
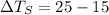
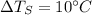
Now,
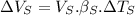
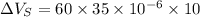

c)
Quantity of gasoline spilled after the given temperature change: