Question

Nt) Consider the two dimensional subspace U of R3 spanned by the set {u1,u2} where u1=⎡⎣⎢3−2−2⎤⎦⎥,u2=⎡⎣⎢690⎤⎦⎥. The orthogonal complement V=U⊥ of UϵR3 is the one dimensional subspace of R3 such that every vector vϵV is orthogonal to every vector uϵU. In other words, u⋅v=0 for all uϵU and vϵV. Find the first two components v1 and v2 of the vector vϵV for which

A. v3=1.
B. v1=
C. v2 =
D. v3=1.

Answer 1

`v_1=(18)/(39), v_2=(-4)/(13)`

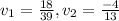
Explanation:

Let
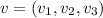`v=(v_1,v_2,v_3)` a vector in the orthogonal complement of U.
`v` satisfies
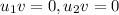`u_1 v=0, u_2v=0`. This means that

`3v_1-2v2-2v_3=0\\6v_1+9v_2+0v_3=0`

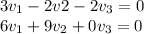
Then, we have a homogeneous system. Since every homogeneous system is consistent, and since we have more unknowns that equations them the system has infinite solutions.

Let's see which is the set of solutions of the system:

The augmented matrix of the system is:

`A=\left[\begin{array}{ccc}3&-2&-2\\6&9&0\end{array}\right]`

We apply row operations for find the echelon form of A:

1. To the second row of A we subtract the first row twice and we obtain:

`\left[\begin{array}{ccc}3&-2&-2\\0&13&4\end{array}\right]`

Now we apply backward substitution:

1.

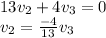
`13v_2+4v_3=0\\v_2=(-4)/(13)v_3`

2.

`3v_1-2v_2-2v_3=0\\3v_1-2((-4)/(13))v_3-2v_3=0\\3v_1=(18)/(13)v_3\\v_1=(18)/(39)v_3`

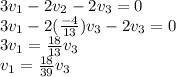
Then the set of solutions is

`\{(v_1,v_2,v_3)=((18)/(39)v_3,(-4)/(13)v_3,v_3)\}`

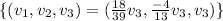
Since we need the vector v such that
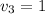`v_3=1`, then we replace in the above equations and we obtain the coordinates
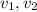`v_1, v_2`.

`v_1=(18)/(39)v_3=(18)/(39)*1=(18)/(39)\\v_2=(-4)/(13)v_3=(-4)/(13)*1=(-4)/(13)`