Question

A local farmer has been selling boxes of imperfect produce. Suppose the first week he sold 50pounds of produce the second week he sold 60 pounds and the third week he sold 72 pounds.

Assuming that the imperfect produce sales followed a consistent pattern of growth, how many pounds of produce were sold the 20th week? Round your answer to the nearest whole number.​

Answer 1

• 1,597 pounds

Step-by-step explanation:

To find the pattern, write the number of boxes sold each week in the form of a sequence:

• 50, 60, 72, . . .

The two simplest sequences are arithmetic and geometric sequences.

Arithmetic sequences are consecutive numbers that keep a constant difference. In this case 60 - 50 = 10 and 72 - 60 = 12, so the consecutive numbers do not have a constant difference and they to do not form an arithmetic sequence.

Geometric sequences are consecutive numbers that keep a constant ratio. In this case 60 / 50 = 1.2, and 72 / 60 = 1.2. So, assuming that the patttern of growth is consistent, they form a geometric sequence with ratio = 1.2.

The general term for a geometric sequence is given by the formula:

• 
  `a_n=a_0r^{n-1`

Here:

`a_0=50\\ \\ r=1.2`

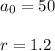
And you need to calculate the 20th term:

• 
  `a_(20)=50(1.2)^(20-1)=50(1.2)^(19)=1,597.4=1,597`