Answer:
80.0°C will be the final temperature inside the calorimeter.
Step-by-step explanation:
Heat lost by the pace of jewelry will be equal to heat gained by the another piece of the jewelry

Mass of piece-1=
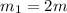
Specific heat capacity of copper=
 = 0.387 J/g.K
= 0.387 J/g.K
Initial temperature of the iron =
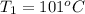
Final temperature =
 =T
=T
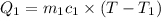
Mass of piece-2=
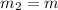
Specific heat capacity of copper =
 = 0.387 J/g.K
= 0.387 J/g.K
Initial temperature of the water =
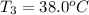
Final temperature of water =
 =T
=T
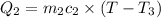
 (conservation of energy)
(conservation of energy)

On substituting all values:
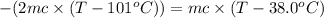

80.0°C will be the final temperature inside the calorimeter.