Question

Suppose a bag contains 4 white chips and 6 black chips. What is the probability of randomly choosing a black chip, not replacing it, and then randomly choosing another black chip?

A. 9/25
B. 4/25
C. 1/3
D. 2/15

Answer 1

1/3

Explanation:

product of probability of choosing black in first pick and second pick

6/10*5/9=1/3

Answer 2

Option C

The probability of randomly choosing a black chip, not replacing it, and then randomly choosing another black chip is
`(1)/(3)`

Solution:

A bag contains 4 white chips and 6 black chips .

So, total number of chips are 10

We have to find the probability of randomly choosing a black chip, not replacing it, and then randomly choosing another black chip

Let A be the event of randomly choosing a black chip out of total 10 chips can be written as:-

`\mathrm{P}(\mathrm{A})=\frac{\text { Possible number of Black chips }}{\text { Total number of chips }}`

`\mathrm{P}(\mathrm{A})=(6)/(10)=(3)/(5)`

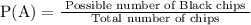
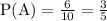
Let B be the next successive event in which the black chip is not replaced, so we are left with 4 White chips and 5 Black Chips

Now the probability of happening this event is :

`\mathrm{P}(\mathrm{B})=\frac{\text { Possible number of Black chips }}{\text { Total number of chips }}`

`\mathrm{P}(\mathrm{A})=(5)/(9)`

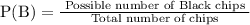
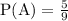
Since, these are successive cases so total probability is:

`=(3)/(5) * (5)/(9)=(1)/(3)`

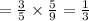
Hence, the probability of happening given event is
`(1)/(3)`

Thus option C is correct