0.22 is the probability that Keyshawn doesn't get a strike until after his first five attempts.
Solution:
Given: Chance of getting a strike each time is

To find: The probability that Keyshawn doesn't get a strike until after his first five attempts.
Not striking on
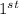 attempt =
attempt =
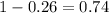
Not striking on
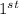 and
and
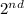 attempt =
attempt =

Not striking upto
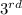 attempt =
attempt =
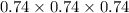
Not striking upto
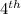 attempt =
attempt =

Not striking upto
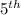 attempt =
attempt =
