Question

A company manufactures televisions in batches of 25 and there is a 1% rate of defects. Find

the standard deviation for the number of defects per batch.
O 0.7
O 0.9
00.5
O 72.8

Answer 1

The standard deviation for the number of defects per batch is 0.5

Solution:

In binomial distribution, standard deviation is given as:

`\sigma=√(np(1-p))`

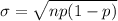
Where "n" is the number of observations

"p" is probability of getting success

We are given that ,

Total batches of televisions : n = 25

The probability of defects : p = 1% = 0.01

Here success is getting defective batch

Then, the standard deviation for the number of defects per batch will be:

Plugging in values in formula, we get

`\sigma=√((25)(0.01)(1-0.01))\\\\=√((25)(0.01)(0.99))\\\\=√(0.2475)\\\\=0.497493718553\approx0.5`

Therefore, the standard deviation for the number of defects per batch = 0.5