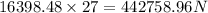Question

An airplane wing is designed so that the speed of the air across the top of the wing is 255 m/s when the speed of the air below the wing is 199 m/s. The density of the air is 1.29 kg/m3. What is the lifting force on a wing of area 27.0 m2?

Answer 1

Answer:442758.96N

Step-by-step explanation:

This problem is solved using Bernoulli's equation.

Let
`P` be the pressure at a point.

Let
`p` be the density fluid at a point.

Let
`v` be the velocity of fluid at a point.

Bernoulli's equation states that
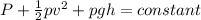`P+(1)/(2)pv^(2)+pgh=constant` for all points.

Lets apply the equation of a point just above the wing and to point just below the wing.

Let
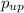`p_(up)` be the pressure of a point just above the wing.

Let
`p_(do)` be the pressure of a point just below the wing.

Since the aeroplane wing is flat,the heights of both the points are same.

`(1)/(2)(1.29)(255)^(2)+p_(up)= (1)/(2)(1.29)(199)^(2)+p_(do)`

So,
`p_(up)-p_(do)=(1)/(2)* 1.29* (25424)=16398.48Pa`

Force is given by the product of pressure difference and area.

Given that area is
`27ms^(2)`.

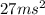So,lifting force is
`16398.48* 27=442758.96N`