Question

Farmer Theresa's Produce Stand sells 27.5 lbs. bags of mixed nuts that contain 44% peanuts. To make her product she combines Brand A mixed nuts which contain 20% peanuts and Brand B mixed nuts which contain 70% peanuts. How much of each does she need to use?

Answer 1

Theresa needs 14.3 pounds of Brand A mixed nuts and 13.2 pounds of Brand B mixed nuts.

Explanation:

Let A represent the brand A mixed nuts and B represent Brand B mixed nuts.

We have been given that farmer Theresa's Produce Stand sells 27.5 lbs. bags. We can represent this information in an equation as:

`A+B=27.5...(1)`

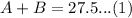
We are also told that to make her product she combines Brand A mixed nuts which contain 20% peanuts and Brand B mixed nuts which contain 70% peanuts.

We can represent this information in an expression as:

`0.20A+0.70B`

Since the stand sells 27.5 lbs. bags of mixed nuts that contain 44% peanuts. We can represent this information in an equation as:

`0.20A+0.70B=0.44(27.5)...(2)`

Upon substituting equation (1) in equation (2), we will get:

`0.20(27.5-B)+0.70B=0.44(27.5)`

`5.50-0.20B+0.70B=12.10`

`5.50+0.50B=12.10`

`5.50-5.50+0.50B=12.10-5.50`

`0.50B=6.6`

`(0.50B)/(0.50)=(6.6)/(0.50)`

`B=13.2`

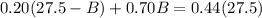
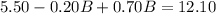
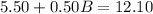
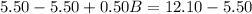
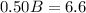
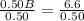
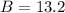
Therefore, Theresa needs 13.2 pounds of Brand A mixed nuts.

To find amount of Brand B mixed nuts, we will substitute
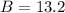`B=13.2` in equation (1) as:

`A+13.2=27.5`

`A+13.2-13.2=27.5-13.2`

`A=14.3`

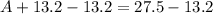
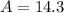
Therefore, Theresa needs 14.3 pounds of Brand B mixed nuts.